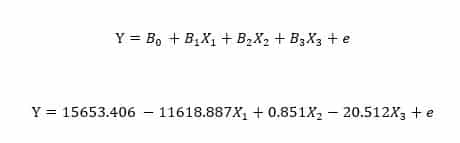Multiple Regression SPSS GSSS Dataset
Multiple Regression SPSS GSSS Dataset Project – Multiple regression is a statistical analysis technique used to examine the relationship between a dependent variable (the outcome or response variable) and two or more independent variables (predictors or explanatory variables). In other words, it allows you to predict the value of the dependent variable based on the values of the independent variables.
SPSS (Statistical Package for the Social Sciences) is a widely used software for statistical analysis in various fields, including social sciences, business, and other research domains. It provides tools to perform a wide range of statistical analyses, including multiple regression.
The GSS (General Social Survey) dataset is a well-known dataset in the social sciences, particularly in sociology. The GSS is a survey conducted in the United States that collects data on a wide range of topics, such as demographics, attitudes, and behaviors. Researchers use the GSS dataset to analyze trends and relationships in society.
Multiple Regression Background
A “Multiple Regression SPSS GSSS Dataset” refers to the application of multiple regression analysis using the GSS dataset within the SPSS software. This could involve analyzing the relationship between one or more dependent variables (e.g., income, happiness, political affiliation) and several independent variables (e.g., age, education, gender) using the GSS dataset and the statistical capabilities of SPSS.
Research question:
The effect of age, number of children, respondent’s income and weekly working hours on the overall family income.
Research hypothesis:
H0: age, number of children, respondent’s income and weekly working hours has no effect on the family’s income.
H1: age, number of children, respondent’s income and weekly working hours has an effect on the family’s income.
Research design:
The research design adopted in this study is referred to as causal relationship approach with the aim of analyzing the effect of age, number of children, respondent’s income and weekly working hours on the overall family income. According to (Cooper & Schindler, 2014), the main concern in causal relationship approach is with how one variable(s) affects or is responsible for changes in another variable(s).
Dependent variable:
The dependent variable(Y) used was the family income. The income was measured in constant dollars showing how much income the whole family generates.
Independent variables:
(X1) the first independent variable is the number of children in each family
(X2) respondent’s income measured in constant dollars is the second variable
(X3) weekly working hours is the last independent variable which is measured by the number of hours the respondent works in a week.
Control variables:
Control variables are the held constant in order to assess the relationship between other variables (Allison, P. D., 1990). This research has included two control variable which are the sex of the respondents and their ages. These variables are added because in a typical society the sex affects the income of the worker and the higher the age the greater the experience hence increased income. By setting the two variable as control we excluded their effect on the model.
| Descriptive Statistics | |||
| Mean | Std. Deviation | N | |
| FAMILY INCOME IN CONSTANT DOLLARS | 56199.86 | 48030.037 | 32 |
| NUMBER OF HOURS USUALLY WORK A WEEK | 39.69 | 12.880 | 32 |
| NUMBER OF CHILDREN | 2.59 | 1.720 | 32 |
| RESPONDENT INCOME IN CONSTANT DOLLARS | 31446.56 | 30660.828 | 32 |
| AGE OF RESPONDENT | 47.88 | 12.289 | 32 |
| RESPONDENTS SEX | 1.69 | .471 | 32 |
| Model Summary | |||||||||
| Model | R | R Square | Adjusted R Square | Std. Error of the Estimate | Change Statistics | ||||
| R Square Change | F Change | df1 | df2 | Sig. F Change | |||||
| 1 | .744a | .554 | .468 | 35040.004 | .554 | 6.449 | 5 | 26 | .001 |
| a. Predictors: (Constant), RESPONDENTS SEX, AGE OF RESPONDENT, NUMBER OF HOURS USUALLY WORK A WEEK, NUMBER OF CHILDREN, RESPONDENT INCOME IN CONSTANT DOLLARS | |||||||||
| Coefficients | ||||||
| Model | Unstandardized Coefficients | Standardized Coefficients | T | Sig. | ||
| B | Std. Error | Beta | ||||
| 1 | (Constant) | 15653.406 | 51982.735 | .301 | .766 | |
| AGE OF RESPONDENT | 1684.865 | 667.954 | .431 | 2.522 | .018 | |
| NUMBER OF CHILDREN | -11618.887 | 4835.608 | -.416 | -2.403 | .024 | |
| RESPONDENT INCOME IN CONSTANT DOLLARS | .851 | .330 | .543 | 2.579 | .016 | |
| NUMBER OF HOURS USUALLY WORK A WEEK | -20.512 | 767.766 | -.006 | -.027 | .979 | |
| RESPONDENTS SEX | -21296.312 | 16254.030 | -.209 | -1.310 | .202 | |
| a. Dependent Variable: FAMILY INCOME IN CONSTANT DOLLARS | ||||||
Results:
A multiple regression test was carried out to test if number of children in a family, respondent’s income and number of hours worked weekly affect the overall family income. From the SPSS output the independent variable affect the dependent variable. The model summary table show that r=0.74, r2=0.554 thus, there is a positive correlation between the predictor and the response variables.
Additionally, 55.4% of the variation in the family income (M= 56199.86, SD= 48030.037, N= 32) is explained by variations in the dependent variables. From the f value F= 6.449, p=0.001, the f change tests for overall significance of the independent variable in the model and p value< 0.05 we therefore reject the null hypothesis (Anderson et al., 2000) and conclude that the independent variable are statistically significance hence they affect the family income.
The coefficient tables gives rise to the models regression equation:
Where:
Y= family income in constant dollars
X1= number of children in the family
X2= respondent’s income in constant dollars
X3= number of hours worked weekly.
e= noise
X1 (M=2.59,SD=1.720,N=32) is statistically significant at t=-2.403,p=0.024 because the p value is less than 0.05, the effect size is at -11618.887 such that an increase in children number in the family ceteris paribus leads to a decrease in family income by 11618.887dollars.
X2(M=31446.56, SD=30660.828, N=32) is also statistically significant at t=2.579, p= 0.016 being less than 0.05 we reject the null hypothesis and conclude that the respondent’s income affects the family income. The effect size is such that an increase in the respondent’s income by one dollar ceteris paribus leads to an increase in the family income by 0.851.
X3(M=39.69, SD=12.880,N=32) is not statistically significant, t=-0.027, p=0.979,the p-value being greater than 0.05 we accept the null hypothesis that respondent’s number of weekly working hours does not affect the family’s income.
In conclusion we establish from the statistics that, other than sex and age of the respondent the family’s income is affected by the number of children in the family and the respondent’s income holding other factors constant.
References
Allison, P. D. (1990). Change Scores as Dependent Variables in Regression Analysis. Sociological Methodology, 20, 93.
Cadotte, M. W., & Davies, T. J. (2018). Randomizations, Null Distributions, and Hypothesis Testing. Princeton University Press.
Cooper, D. R., & Schindler, P. S. (2014). Business Research Methods. New York, NY: McGraw Hill Education.
David, Anderson R., Burnham, K. P., & Thompson, W. L. (2000). Null hypothesis testing: Problems, prevalence, and an alternative. Journal of Wildlife Management, 64(4), 912-923
Relevant Multiple Regression SPSS Posts
Statistics Project – Comparing Two Populations
Did you find any useful knowledge relating to multiple regression SPSS GSSS datasets in this post? What are the key facts that grabbed your attention? Let us know in the comments. Thank you.